GoogleCTF 2024 DESFUNCTIONAL Writeup

2024-06-24

I took a shot at GoogleCTF solo this year, with the goal of solving a flag and doing writeup. I've been a regular and have won prices at my university's CTF which ranges from beginner to intermediate challenges. I wanted to find a more advanced challenge around my skill level, not for prizes but more as a learning opportunity.

I've always been strong in cryptography so I focused on the DESFUNCTIONAL challenge.

Challenge description

A newbie firend of mine was tring to implement a secure server for DES encryption and decrpytion but there seem to be some errors unexpectedly creeping in the key. It is getting frustrating, please help

chall.py attachment

# Copyright 2024 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
#     https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.

import signal
import os
import random
import sys
from Crypto.Cipher import DES3


class Desfunctional:
    def __init__(self):
        self.key = os.urandom(24)
        self.iv = os.urandom(8)
        self.flipped_bits = set(range(0, 192, 8))
        self.challenge = os.urandom(64)
        self.counter = 128

    def get_flag(self, plain):
        if plain == self.challenge:
            with open("flag.txt", "rb") as f:
                FLAG = f.read()
            return FLAG
        raise Exception("Not quite right")

    def get_challenge(self):
        cipher = DES3.new(self.key, mode=DES3.MODE_CBC, iv=self.iv)
        return cipher.encrypt(self.challenge)

    def corruption(self):
        if len(self.flipped_bits) == 192:
            self.flipped_bits = set(range(0, 192, 8))
        remaining = list(set(range(192)) - self.flipped_bits)
        num_flips = random.randint(1, len(remaining))
        self.flipped_bits = self.flipped_bits.union(
            random.choices(remaining, k=num_flips))
        mask = int.to_bytes(sum(2**i for i in self.flipped_bits), 24)
        return bytes(i ^ j for i, j in zip(self.key, mask))

    def decrypt(self, text: bytes):
        self.counter -= 1
        if self.counter < 0:
            raise Exception("Out of balance")
        key = self.corruption()
        if len(text) % 8 != 0:
            return b''
        cipher = DES3.new(key, mode=DES3.MODE_CBC, iv=self.iv)
        return cipher.decrypt(text)


if __name__ == "__main__":
    chall = Desfunctional()
    PROMPT = ("Choose an API option\n"
              "1. Get challenge\n"
              "2. Decrypt\n"
              "3. Get the flag\n")
    signal.alarm(128)
    while True:
        try:
            option = int(input(PROMPT))
            if option == 1:
                print(chall.get_challenge().hex())
            elif option == 2:
                ct = bytes.fromhex(input("(hex) ct: "))
                print(chall.decrypt(ct).hex())
            elif option == 3:
                pt = bytes.fromhex(input("(hex) pt: "))
                print(chall.get_flag(pt))
                sys.exit(0)
        except Exception as e:
            print(e)
            sys.exit(1)

Understanding the script

The script takes input for three options:

Choose an API option
1. Get challenge
2. Decrypt
3. Get the flag

Lets work backwards.

Our flag is read by option 3 get_flag(self, plain).

if plain == self.challenge the flag is read.

self.challenge = os.urandom(64) is a random 64 bytes. We'll need to determine the value of the challenge plaintext to retrieve the flag.

Option 1 get_challenge(self) returns the ciphertext of challenge encrypted with 3DES.

Option 2 decrypt(self, text: bytes) will return the plaintext of a 3DES encrypted ciphertext. But the decrypt key = self.corruption()

The corruption function returns an XOR of self.key and a pseudo random generated mask

flipped_bits is a list of indexes of which bits are flipped. It starts with the last bit (every 8th bit) of each byte flipped.

Lets add

print(" ".join(f"{byte:08b}" for byte in mask))

to print the mask in binary to see what it looks like.

Add this to main

for i in range(16):
    print(i)
    chall.corruption()

0
01000101 00000011 00000001 00001011 00100011 00000001 01100001 01000001 00101001 00000001 01010001 10010001 00000101 01000101 11001001 10001101 00000001 00000001 10001001 00100001 01000001 01100101 00000001 10000001
1
11101111 01110111 11110011 10011011 11101111 10011101 11101101 11101101 01111101 01101011 01110101 11011111 01101101 11110101 11111111 10011111 00101001 10010011 11011011 01111011 11110011 11100111 01001101 10011111
2
11101111 01110111 11111011 10011011 11101111 10011101 11101101 11101101 01111101 01101011 01110101 11011111 01101101 11110101 11111111 10011111 00101001 10010011 11011011 01111011 11111011 11100111 01001101 10011111
3
11101111 11110111 11111111 11111011 11101111 11011101 11101111 11101111 01111101 11111111 01110111 11111111 01111101 11110101 11111111 10011111 11111101 10011111 11011111 01111111 11111011 11100111 11101101 10111111
4
11101111 11111111 11111111 11111011 11111111 11111101 11101111 11111111 11111111 11111111 01110111 11111111 11111101 11110111 11111111 11111111 11111101 11011111 11011111 11111111 11111011 11110111 11111101 11111111
5
11101111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 01110111 11111111 11111111 11111111 11111111 11111111 11111101 11111111 11011111 11111111 11111111 11110111 11111101 11111111
6
11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 01111111 11111111 11111111 11111111 11111111 11111111 11111101 11111111 11111111 11111111 11111111 11111111 11111111 11111111
7
11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 01111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111
8
11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111
9
10001001 00111001 00000001 01000011 00001001 01000001 00000011 11000001 00000001 00000011 00010101 00010001 00101001 01001101 10000011 10100101 11100011 01000001 10111011 01101111 00001001 00010001 01100101 00001101
10
10001001 10111011 00000011 01101011 00011011 01001011 00000011 11001111 00011001 00100011 00010101 01010101 00101101 11101101 10000111 10110101 11100011 01011001 10111011 01101111 01001001 11010001 01100111 01111111
11
10101101 11111111 11000111 11101011 00011011 01001011 11100111 11101111 11111001 00100011 00110101 11111111 10111111 11111101 11110111 10110101 11100011 11111001 10111011 11101111 01011001 11010011 01110111 01111111
12
11101101 11111111 11000111 11111011 10111111 01001011 11110111 11101111 11111101 11101011 00110101 11111111 10111111 11111111 11110111 11111101 11100011 11111111 10111111 11101111 01011101 11010011 01110111 11111111
13
11101101 11111111 11010111 11111111 10111111 11101111 11111111 11111111 11111111 11111011 10111101 11111111 11111111 11111111 11111111 11111111 11111011 11111111 10111111 11111111 11011111 11111111 01111111 11111111
14
11101111 11111111 11111111 11111111 11111111 11101111 11111111 11111111 11111111 11111011 11111101 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111
15
11101111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111101 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111

self.flipped_bits persists between corruption()s. Additional bits are flipped using the previous value until all bits are flipped, and then flipped_bits returns to it's original value.

if len(self.flipped_bits) == 192:
    self.flipped_bits = set(range(0, 192, 8))

Given enough iterations (can be seen at i=8) mask always becomes

11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111

This means the decrypt() function should inevitibly use the compliment of self.key

DES exhibits the complementation property, namely that

DES being symmetric, the complementation property applies to decrypting as well.

Taking the complement of ciphertext from get_challenge(), and decrypt() it when the key is in the complement state, I should get the complement of challenge.

The first 8 bytes will need to be complemented again, because in CBC mode

The first block is XORed with IV, subsequent blocks are XORed with the previous block's ciphertext.

So when you decrypt with the all-bits-flipped key, the intermediate result before XORing with the IV is the complement of what it should be. Since the IV remains the same, you need to complement the result to get the correct first block.

For subsequent blocks, the XOR with the previous ciphertext block (which wasn't affected by the key corruption) naturally corrects this complementation effect.

get_flag() will sys.exit(0) and I'll get Not quite right, which will reset challenge. Let's keep trying the 8th decrypt() until it works.

Solve

Get challenge ciphertext

Choose an API option
1. Get challenge
2. Decrypt
3. Get the flag
1
d7fb309d5a3ac2f3e916c73957d110a3d546491bfd75ccec6eb544347185cbad5dfd58e72e2eed02b2ccbe260ad572497f21d9bd44069c1234ae4e5e5f10d2e2

Compute the complement cipher text 2804cf62a5c53d0c16e938c6a82eef5c2ab9b6e4028a3313914abbcb8e7a3452a202a718d1d112fd4d3341d9f52a8db680de2642bbf963edcb51b1a1a0ef2d1d

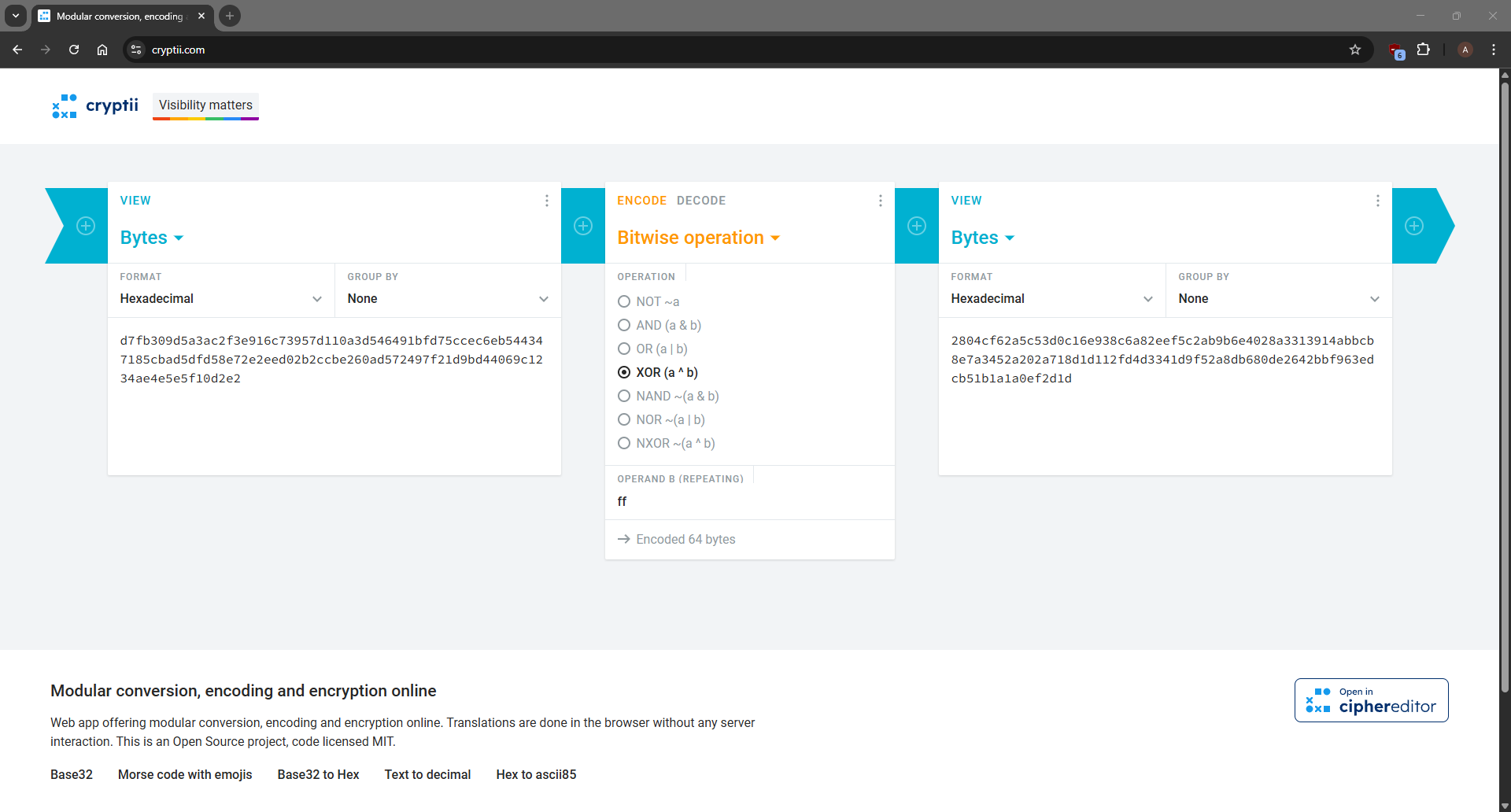
Decrypt until lucky

Choose an API option
1. Get challenge
2. Decrypt
3. Get the flag
2
(hex) ct: 2804cf62a5c53d0c16e938c6a82eef5c2ab9b6e4028a3313914abbcb8e7a3452a202a718d1d112fd4d3341d9f52a8db680de2642bbf963edcb51b1a1a0ef2d1d
33688802886637db3b0f8dd997c8fd0be42a3ce44205f326fc0456e0c1654f1162fba220266a91a1930e61aeffb3ce93a4f5fa58af893c8c3c58ef4574fd86d8
Choose an API option
1. Get challenge
2. Decrypt
3. Get the flag
2
(hex) ct: 2804cf62a5c53d0c16e938c6a82eef5c2ab9b6e4028a3313914abbcb8e7a3452a202a718d1d112fd4d3341d9f52a8db680de2642bbf963edcb51b1a1a0ef2d1d
3bbd1f34a492ff8fb1370369d19d40f62803a0fb64ebc7427426bb335cfca606b7138afed101135c069656dd053151876867aab9712ab7ab82c7e8b573f6f58a
Choose an API option
1. Get challenge
2. Decrypt
3. Get the flag
2
(hex) ct: 2804cf62a5c53d0c16e938c6a82eef5c2ab9b6e4028a3313914abbcb8e7a3452a202a718d1d112fd4d3341d9f52a8db680de2642bbf963edcb51b1a1a0ef2d1d
5d98dfa2b47e298a65805ca7c478246ff23b44071e2a00431b82610254e9dc09bdc919cb766a8ac9a93b179f8203214b57b2b6947d81adec1e34a0ccdc2d9030
Choose an API option
1. Get challenge
2. Decrypt
3. Get the flag
2
(hex) ct: 2804cf62a5c53d0c16e938c6a82eef5c2ab9b6e4028a3313914abbcb8e7a3452a202a718d1d112fd4d3341d9f52a8db680de2642bbf963edcb51b1a1a0ef2d1d
79910b8da4ab535386ae5fa75535b34aae174a1ab37e8c7469c25e609ffca7fbe013796e95552bd389e38d3c89ef92718814e681948fc0b54ef819d30467d4dd
Choose an API option
1. Get challenge
2. Decrypt
3. Get the flag
2
(hex) ct: 2804cf62a5c53d0c16e938c6a82eef5c2ab9b6e4028a3313914abbcb8e7a3452a202a718d1d112fd4d3341d9f52a8db680de2642bbf963edcb51b1a1a0ef2d1d
e284a92a0dae7a43e5911c2c7994e859bab57d7012bf443766fb03516daad0c44757b89040ac56736bf6697c24c2e9be2b6850d87c5b4d0d734e14ebb3361afd
Choose an API option
1. Get challenge
2. Decrypt
3. Get the flag
2
(hex) ct: 2804cf62a5c53d0c16e938c6a82eef5c2ab9b6e4028a3313914abbcb8e7a3452a202a718d1d112fd4d3341d9f52a8db680de2642bbf963edcb51b1a1a0ef2d1d
fec5bcd64752cb713bb8dea376d67ab0dc9948137b94a503e9ea9701bab73b46764ee442b63260294bc862326e23ea4408037511edc6db77a367af59659f626b
Choose an API option
1. Get challenge
2. Decrypt
3. Get the flag
2
(hex) ct: 2804cf62a5c53d0c16e938c6a82eef5c2ab9b6e4028a3313914abbcb8e7a3452a202a718d1d112fd4d3341d9f52a8db680de2642bbf963edcb51b1a1a0ef2d1d
7ff31c047fd84d0b47706b119bf9398aa595138ef523428db8282cb70afca61742a75d04d800f7b6eb068cf15f61a6f83f16680b68f563bb73f5e7c7910e6b40
Choose an API option
1. Get challenge
2. Decrypt
3. Get the flag
2
(hex) ct: 2804cf62a5c53d0c16e938c6a82eef5c2ab9b6e4028a3313914abbcb8e7a3452a202a718d1d112fd4d3341d9f52a8db680de2642bbf963edcb51b1a1a0ef2d1d
4058ca05a13a4c9f00c989e10b3d9ed1e68af5dd26cd90dcaaeb7db69f6582b195a3ea8272e2d523cfb2c5d2bd1830923eefc25f2444e708c64ab8cd249115fc

Compute the complement of the first 8 bits bfa735fa5ec5b360

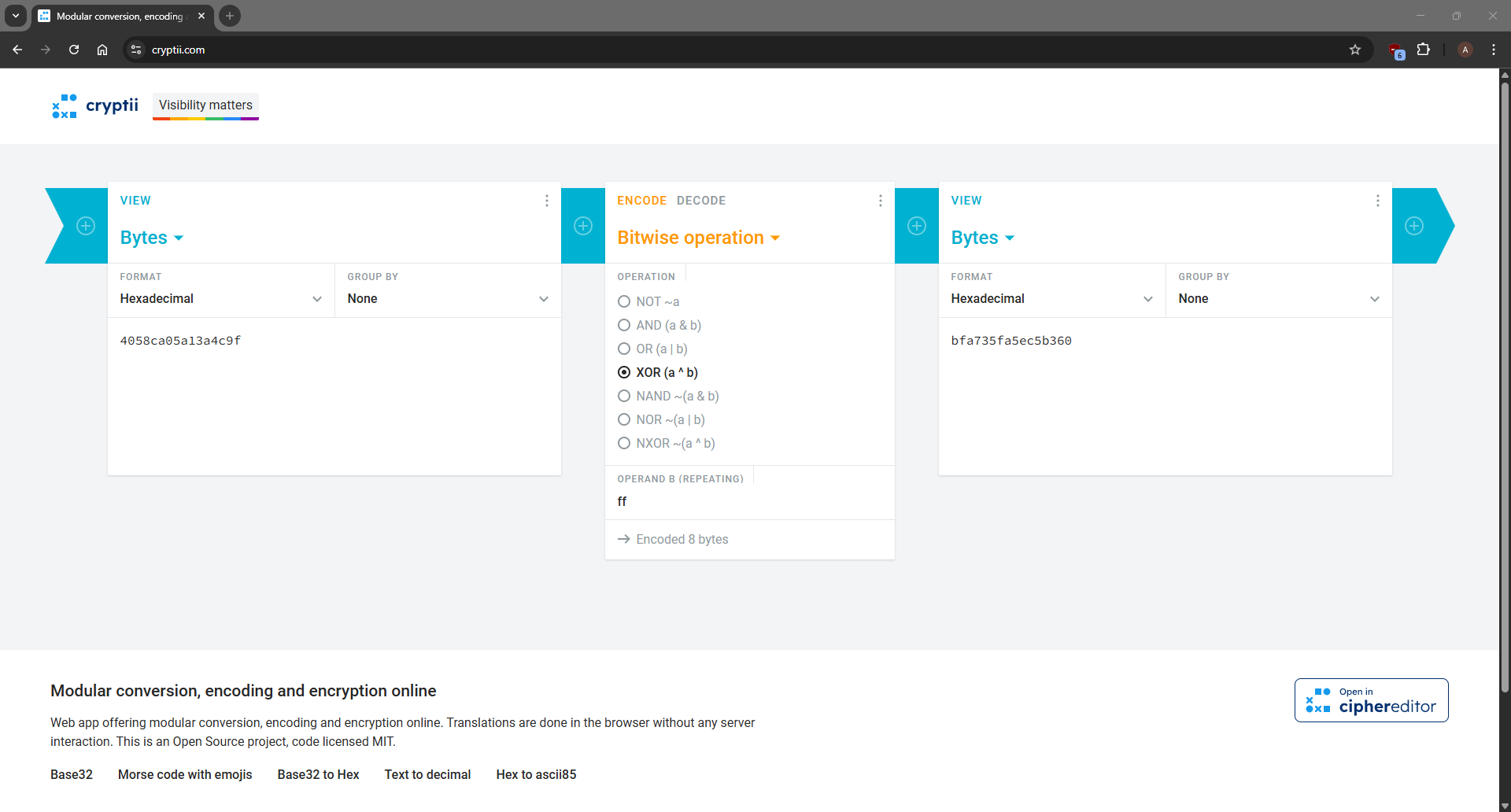
Use it to form challenge bfa735fa5ec5b36000c989e10b3d9ed1e68af5dd26cd90dcaaeb7db69f6582b195a3ea8272e2d523cfb2c5d2bd1830923eefc25f2444e708c64ab8cd249115fc

Get the flag

Choose an API option
1. Get challenge
2. Decrypt
3. Get the flag
3
(hex) pt: bfa735fa5ec5b36000c989e10b3d9ed1e68af5dd26cd90dcaaeb7db69f6582b195a3ea8272e2d523cfb2c5d2bd1830923eefc25f2444e708c64ab8cd249115fc
CTF{y0u_m4y_NOT_g3t_th3_k3y_but_y0u_m4y_NOT_g3t_th3_c1ph3rt3xt_as_w3ll}